2020-05-05

复杂链表的复制

问题描述

请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null

来源：LeetCode(https://leetcode-cn.com/problems/fu-za-lian-biao-de-fu-zhi-lcof)
图片参考：CyC2018

解法一

2020-05-05

滑动窗口的最大值

问题描述

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

进阶：
你能在线性时间复杂度内解决此题吗？
示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

来源：LeetCode

解法一

首先看暴力解法，设nums的长度为n，则主循环遍历n-k+1次，子循环k次，即可完成对每个窗口的求解，时间复杂度是O(nk)。根据窗口的定义，我们只需要维护窗口的元素，并提供一个接口，查询当前窗口的最大值。维持大小为k的大顶堆可以查询最大值，但在维护窗口上，删除上一个窗口的第一个元素，需要花费的时间不得而知，因为堆只是维持父子节点的弱有序，查询的复杂度是不确切的。

因为在窗口滑动时，我们需要删除上一个窗口的第一个元素，且最好能在O(1)的时间里删除，则可以尝试队列，同时，为了提供查询窗口最大值的接口，我们把front设置成最大值的索引，front到back的元素是小于front的元素。这里使用索引而不是最大值，是因为如果是最大值，我们无法确认是否front是否还在当前窗口内。front的维护方法，窗口移动得到的新元素与队列中的back比较，如果比back大，则弹出back（这里用到pop_back，所以用的队列就是双端队列），因为back不可能是最大值，堵在队列中会影响front（试想front因为窗口滑动而退出，此时新的front是较小的元素，那么front就不是最大值了）。

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> res;
        int n = nums.size();
        if(n == 0 || k == 0 || n < k) return res;
        deque<int> q;
        // 用下标是因为 如果用元素值 则不知道front元素是否在当前窗口范围内
        // front保存最大值 是为了每次能通过front接口得到窗口的最大值
        // [front, back1, back2] front始终保存最大值 如果当前值比back大 则while弹出back
        for(int i = 0; i < k; i++) {
            while(!q.empty() && nums[i] > nums[q.back()]) {
                q.pop_back();
            }
            q.push_back(i);
        }
        res.push_back(nums[q.front()]);
        for(int i = k; i < n; i++) {
            // 之前的最大值是否还在当前窗口内
            if(!q.empty() && q.front() == i-k) { // i=3 k=3 i-k=0
                q.pop_front();
            }
            while(!q.empty() && nums[i] > nums[q.back()]) {
                q.pop_back();
            }
            q.push_back(i);
            res.push_back(nums[q.front()]);
        }
        return res;
    }
};

2020-05-02

详解DES加解密

DES(Data Encryption Standards)是一种经典的对称加密技术，由IBM公司在1970s研发，之后被美国国家标准局标准化。在理解DES之前，我们先补充对称加密的基本思想。

对称加密是加解密使用同一个密钥的加密算法，区别于使用公钥和私钥加解密的非对称加密。同时，按照对称加密的密钥特征，分为流密码(stream cipher)和分组密码(block cipher)，前者每次加密数据的一个位或一个字节，后者则每次加密一个固定大小的块，即先把数据分块，再分别用密钥加密。流密码的代表是RC4，分组密钥的代表则是DES和AES。

现代密钥学只对密钥保密，算法是公开的。因为基于算法的保密随着算法的推测或暴露而消失，同时算法不公开，也难以对算法进行讨论和改进。

一个好的密码系统要能够对抗基于统计方法的密码分析(Statistical cryptanalysis)，比如在选择明文攻击和选择密文攻击得到的明文和密文对中，统计明文和密文的规律，根据密文破解明文，另外，还可以通过分析密文和密钥的对应关系，从而破解密钥。

对抗统计分析攻击的方法是，设法使明文的统计特征尽可能的不带入密文，同时使密文和密钥的统计关系尽量复杂，这样攻击者就很难统计出有效的规律，来推断明文和密钥。

在历史上，这种思想早就有了。信息论的先驱香农在1945年的论文《密码学的数学理论》中给出了设计密码系统的基本方法：混淆(confusion)和扩散(diffusion)。混淆是把密钥和密文的统计关系打乱，使得密钥极其微小的改动，都会造成密文的大幅变动；扩散则把明文和密文的统计关系打乱，使得明文极其微小的改动，都会造成密文的大幅变动，换言之，明文的任意部分都会影响密文的所有部分，这让密码分析者难以找到明文到密文的部分模式，因为模式被上述方式抹掉了。

这种明文和密钥的微小改动，所造成的密文大幅变动，就是雪崩效应(avalanche effect)：

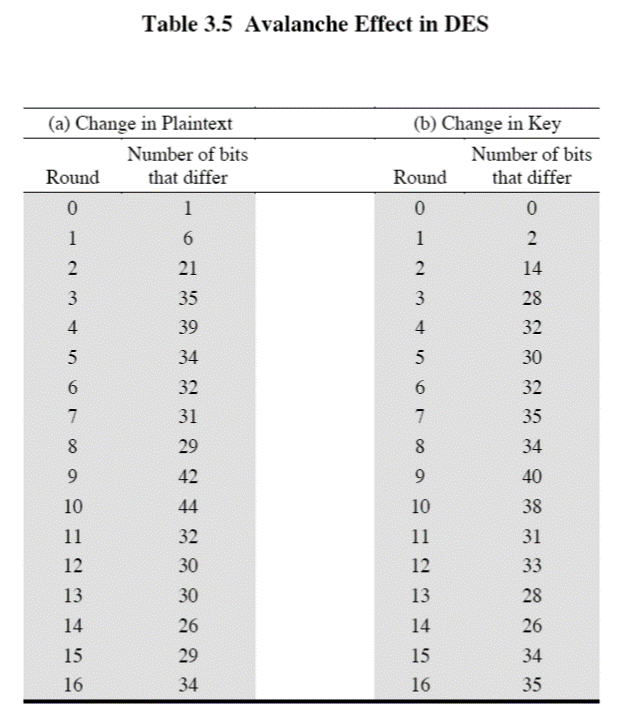
对应到DES的设计，主要是具有雪崩效应的Feistel网络，这是DES的核心，也是后续很多对称加密的核心(如Blowfish、RC5)。

Feistel网络如下：

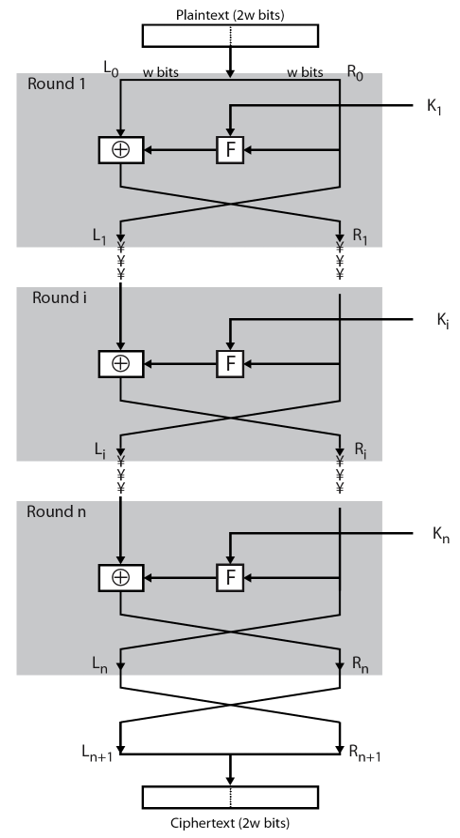
首先说明，DES的分块长度是64位，密钥长度是64位，其中有效密钥的长度是56位，另外的8位用作奇偶校验。DES分块的密文长度是64位。上图的L0和R0分别是64位明文经过初始置换后的左32位和右32位，之后进入16轮的迭代，最后再经过与初始置换的逆置换，来得到最终的密文。

每一轮的具体流程如下：
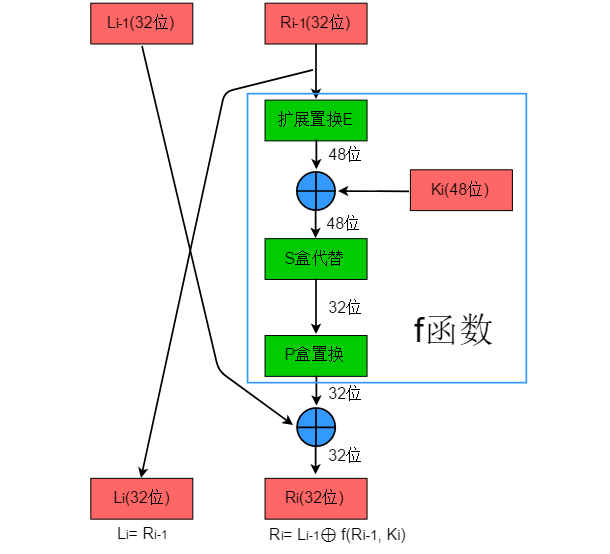
F-function
(来源)

在每轮迭代中，DES都使用相同的加密结构，这种结构就是Feistel结构。公式如下：
$L_i = R_{i-1}$
$R_i = L_{i-1} ⊕ f(R_{i-1}, k_{i-1})$

其中f是feistel函数。每轮除了一些置换(Permutation)外，最核心的是S盒的替代(Substitution)。置换是改变位的顺序，一般使用预置的置换表，替代则通过一定的规则，把数据替代成新的数据。

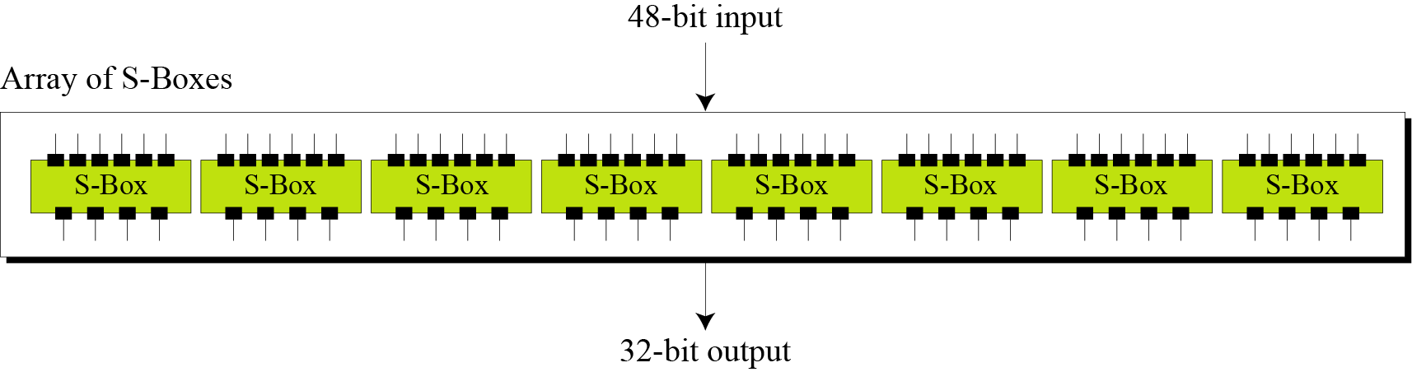
S-Boxes
details

S盒是DES中唯一的非线性部件，S盒的设计从根本上决定了每一轮能否制造足够的复杂性。有了非线性部件，通过多轮迭代，我们就可以得到不断扩散，使得每一轮具有一定随机性的加密输出的每一位，都继续参与下一轮的扩散，结果就是，明文的微小改动，都会经过多轮扩散的放大，最终体现在密文中。(stackoverflow上的解释是：Changing a single bit in the input will cause more bits to be changed in the following rounds.)

关于S盒，如果我们再仔细一点，会发现它的功能是完成6位数据到4位数据的压缩，如果我们得到了4位的S盒输出，想反推出6位的输入，就有四种可能。可以类比一下，当我们知道了密文，想反推出明文，每一轮都有四种可能，4^16次方，那是有多少种可能的明文啊！况且还有密钥的加持。

S盒的作用不仅仅在扩散，因为S盒的输入是每轮密文的Ri和轮密钥Ki，就算不用轮密钥，只使用原始密钥，每次经过非线性的S盒，也会增加混淆的程度。何况为了更好的安全性，DES专门生成了每轮的密钥。

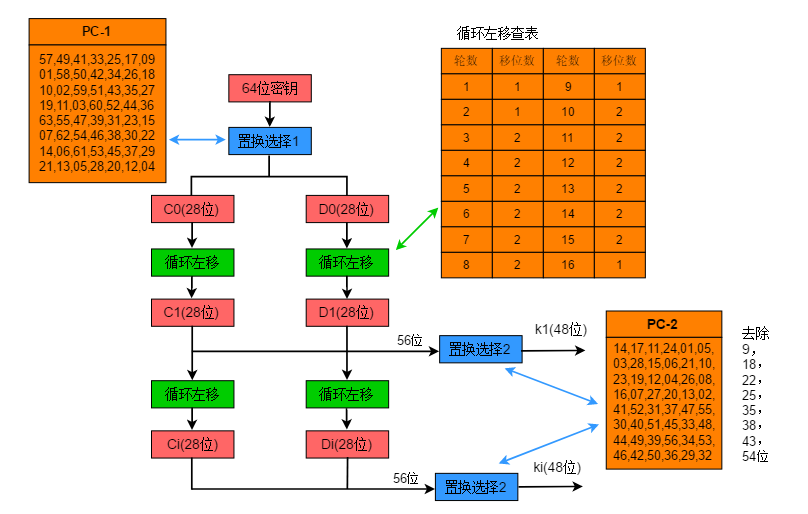
轮密钥生成
(来源)

按照我的理解，轮密钥增加了密钥和密文关系的复杂性，即增加了DES的混淆能力，因为每一位原始密钥的变化，都会通过轮密钥迭代的形式，放大到所生成的所有密钥里。此后，轮密钥与上一轮的加密输出异或后，进入S盒，所以最后的结果是混合了密钥和明文每个位的影响的，就如同蝴蝶效应一样。

分析了DES的Feistel网络的优点，我们来看整个加密流程：
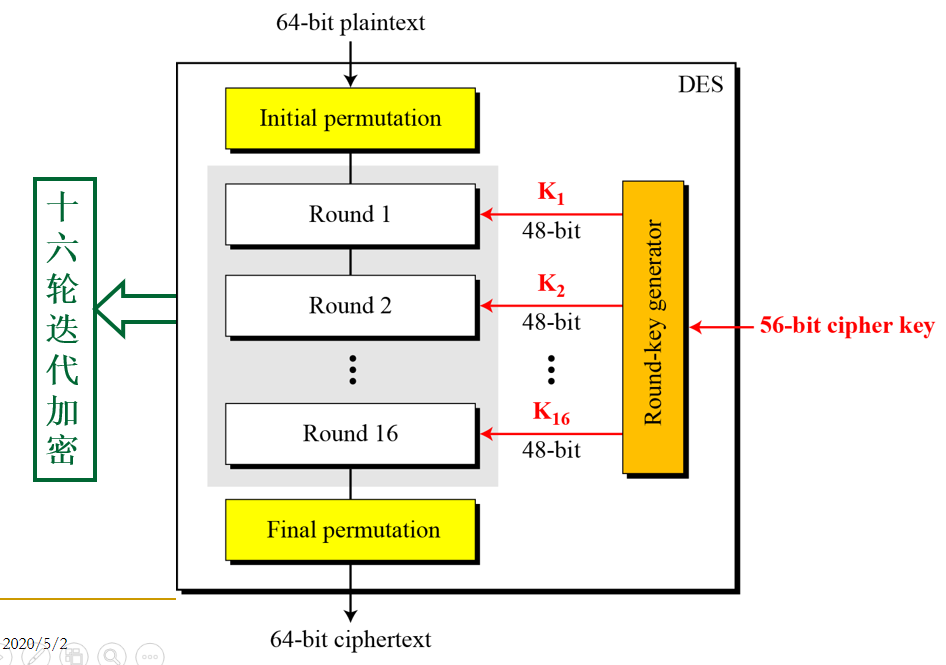
DES加密流程

DES首先了对分组明文做了初始置换(Initial Permutation)，最后结束的时候，对密文做了逆初始置换(Inverse Initial Permutation)。

初始置换

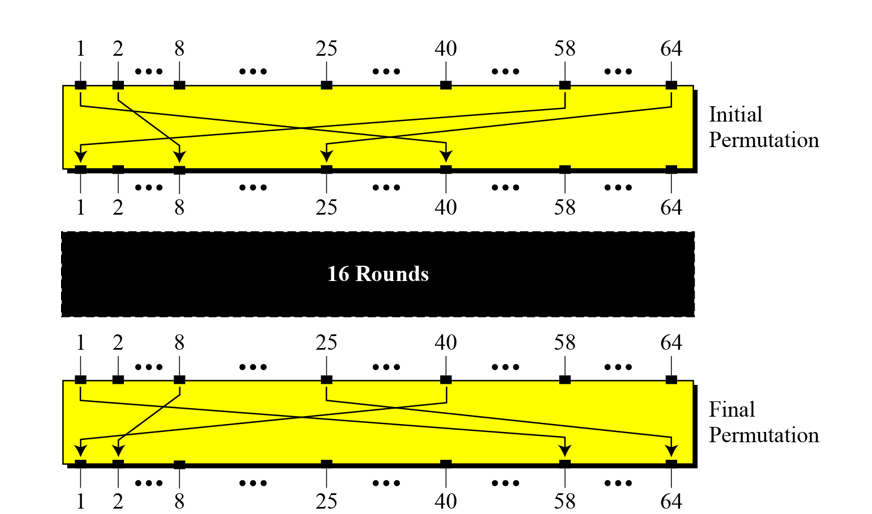
这部分对混淆和扩散没有作用，那为什么还要这两个置换呢？其实这是历史原因，当时DES标准的提交者为了降低硬件实现DES的复杂性，而多了这个设计，所以标准化之后，这个初始置换就留下来了。参见What are the benefits of the two permutation tables in DES?

仔细看的话，会发现后者是把每一位放回到最开始的位置，按照我的理解，这是为了让解密过程也能复用加密的框架。因为解密除了反向使用轮密钥外，其它的过程与加密是一致的。

DES解密是加密的逆过程，上面介绍了初始置换和逆初始置换是逆过程，剩下就是证明16轮迭代解密是16轮迭代加密的逆过程。

这里用到了异或(xor)的重要性质，a⊕a=0, a⊕0=a，考虑一个基本的密码形式，p是明文，c是密钥，e是密文，通过明文和密钥按位异或得到，p⊕c=e，接收方得到密文后，异或密钥解密：e⊕c=p⊕c⊕c=p

每轮解密，我们需要用 $L_i$ 和 $R_i$ ，解密出上一轮的 $L_{i-1}$ 和 $R_{i-1}$

回顾一下加密公式：
$L_i = R_{i-1} \qquad \qquad \qquad \qquad (1)$
$R_i = L_{i-1} ⊕ f(R_{i-1}, k_{i-1}) \ \ \ (2)$

解密公式为：
$L_{i-1} = R_i ⊕ f(L_i, k_{i-1}) \ \ (3)$
$R_{i-1} = L_i \qquad \qquad \qquad \ \ (4)$

把(2)带入到(3)中，则有：
$L_{i-1} = L_{i-1} ⊕ f(R_{i-1}, k_{i-1}) ⊕ f(L_i, k_{i-1})$

再把(4)带入上式：
$L_{i-1} = L_{i-1} ⊕ f(L_i, k_{i-1}) ⊕ f(L_i, k_{i-1}) = L_{i-1}$

这里最后推导出相等，说明按照相同的结构，用下一轮的密文，就可以回推到上一轮密文，最终迭代回明文。只不过这里交换了L和R的顺序，迭代函数的框架可以复用。

写到这里，DES这么经典的算法，的确很经典，Feistel结构，S盒的设计，简单的多轮迭代增加混淆和扩散的思想，都让我感受到DES算法的简洁和经典之美。

PS: 文中如有错误，欢迎指出，本站不胜感激。版权给hackeryard所有，转载请注明出处。

参考：

1.程序员小吴，神秘的DES加密算法

2.nnnnzyx，DES解密是加密的逆过程

3.Wikipedia: Feistel cipher

4.Wikipedia: Confusion and diffusion

5.西电计算机密码学课PPT

2020-05-01

密码保存里的学问

对于用户密码保存，最佳实践是加盐和慢哈希。那为什么要用这种方式？

一般的Web服务器都会在数据库中保存用户名密码，但如果网站存在漏洞而导致脱库，那数据库中的密码就会直接暴露，如果密码以明文的形式保存，那只能说太惨了（参见CSDN密码泄露事件）。

因为哈希函数具有很好的单向性，即已知消息，通过哈希函数能快速计算出对应的摘要，而反过来则困难得多得多，这就是哈希函数的不可逆性。所以可以用哈希函数对密码计算摘要，然后保存在数据库中，这样就算数据库被攻击者拿到了，密码也不会直接暴露。

需要补充的是，服务器拿到前台用户输入的明文密码（HTTPS加密传输），通过计算哈希的方式，与数据库中此用户的摘要比对，如果一致，则验证通过，否则拒绝登录。这里用到了哈希函数的抗碰撞性，即任意两个不同的数据，其摘要相同的可能性极低，或者换一种表述，对于一个数据P1，很难构造与P1不同的数据P2，使得Hash(P2)=Hash(P1)。所以只要匹配到了摘要相等，就可以认为密码是正确的。

但因为对于选定的哈希函数（如常用的MD5、SHA-1、SHA-512），数据和摘要是一一对应的，所以攻击者想到了针对所有数据，依次计算出相应的摘要，然后把摘要作为key，数据作为value，存储起来，这就是彩虹表(Rainbow Table)。彩虹表是一种以空间换时间的方法，同时使用了更多的技术，稍后补充。

攻击者利用现有的彩虹表，一般可以获得对常用用户密码快速的破解，因此需要寻求对抗的方法。需要注意，这里的破解是针对整个用户表，也即所有用户的破解，是一种无差别攻击。按照成本收益考虑，攻击的成本就是下载或构造彩虹表，以及匹配的成本，这种成本在当今的算力和存储成本下是较少的，同时，收益是破解所有用户密码带来的收益，如果用户够多，则单个用户的成本收益比会降低很多。

因为在安全领域，如果攻击一个东西的成本收益不匹配，那么攻击者就是自找没趣。所以问题在于，我们能不能提高单个用户的成本收益比？既然之前是对所有用户都无差别地计算哈希，那我们能不能加点东西，把无差别攻击降级为针对性攻击呢？

这就是加盐：即对每个用户，都生成一个随机字符串(salt)。把salt拼接到密码上，再使用MD5等算法计算哈希，即saltHash=MD5(passwd+salt)。另一种方式是，saltHash=MD5(MD5(passwd),salt)。

这样，就算构造彩虹表，也需要针对每个用户的salt构造，单个用户的成本收益比显著提高了，这就是针对性攻击。

通过加盐，攻击成本大大提高了，但针对短密码，攻击者仍然可以暴力破解，即枚举所有的密码组合，加盐后计算哈希。为了对抗这种攻击，一种慢哈希算法被发明，这就是bcrypt和pdkdf2，拿bcrypt说明，bcrypt有一个cost参数，通过调节cost，可以提高或降低计算哈希的时间，目前bcrypt的时间大概在0.3s，如果未来算力提高，我们可以提高cost，来维持计算哈希的时间不变。对比MD5，暴力破解bcrypt的时间成本非常大，如果是8位字母数字组成的密码，则需要(262 + 10) ^ 8 * 0.3s / (365246060) = 51万年，攻击者早就不知道在哪了。

另外，使用bcrypt后，每次计算都需要0.3s，如果放在后台服务器处理，则需要的计算量是很大的，参考知乎CoderZh的设计，bcrypt可以放在客户端，从而分担服务器的压力，不得不说很巧妙。

这种加盐和慢哈希的方法被用在了很多地方，如Linux的/etc/shadow文件，其中用户密码保存为： $id$ salt$encrypted，id表示具体的哈希函数，encrypted是摘要，我在Ubuntu 18中看到，默认的id=6，对应SHA-512。

在OpenBSD中，则默认使用bcrypt作为密码哈希函数，这里有bcrypt的介绍，有空了看看论文实现。

参考：

1.黄兢成，谈谈密码安全：服务端密码保存

2.CoderZh，加盐密码保存的最通用方法是？

3.密码保存的最佳实践讨论

4.Smallay，什么是彩虹表？

5.Wikipedia: bcrypt

2020-05-01

linux-init

2020-05-01

理解HTTPS协议

2020-04-30

Nginx事件驱动框架

2020-04-29

关于TCP的一切

TCP是传输控制协议的缩写，这里的控制，就是流量控制、拥塞控制和差错控制。TCP是可靠的传输协议，它用了很多机制，来保证传输的可靠性，包括：

1.差错控制

1.1 校验和

检测数据包在传输过程中，是否受到破坏，如果被破坏，接收方会丢弃数据包，并等待数据包超时重传。

1.2 序列号

对每个字节编号，是TCP的核心。TCP基于序列号，实现了对每个字节的发送、接收和确认应答，接收方据此实现了对乱序包的重排序，另外，对重复接收的数据包，接收方会知道这是重复的包，会直接丢弃而不会对已有数据造成影响（如果不对字节编号，那么重复收到的数据包，可能被当做新数据包处理）。

序列号是滑动窗口机制的基础，将在1.5节介绍。

1.3 确认应答机制

因为网络是不可靠的，确认应答可以帮助接收方确切地知道ACK号之前的字节序列都已经收到了。

1.4 超时重传

重传有两种，这一节只介绍超时重传，快速重传在拥塞控制中介绍。
TCP会维护一个RTO(Retransmission TimeOut)，即超时重传计时器，针对每一个发送出去的数据包，都会维护一个RTO，当RTO超时到达，但还没有接收到相应的ACK时，发送方就会重传这个数据包（由此可知，在发送方窗口的左侧，是已发送，未接收ACK确认的数据，这些数据需要一直保存，直到这些数据被确认为止，此时窗口的左边界开始右移，称为滑动）

超时重传要解决的问题是，a.如果发送的数据包在链路中丢失了，接收方没有收到，发送方能在RTO超时后，估计出是数据包丢失了，就会重传；b.确认应答报文ACK也有可能丢失，TCP的设计是把超时重传放在发送方，如果超时，发送方重传数据包，接收方发现这是重复的数据，就知道是ACK丢失了，就会丢弃它，并立即重传ACK。这里之所以把超时重传放在发送方，是因为发送方对数据包丢失和ACK丢失，都可以处理，而接收方感知不到数据包是否丢失，同时，如果要实现对ACK的重传，则需要接收方在ACK重传计时器内发回一个消息（发送方：我收到了你的ACK），这是对ACK的确认，这无疑增加了TCP的复杂性。

这里还有一个问题，如果没有超时重传，会发生什么？那么发送方在发送一个数据包后，如果丢包，接收方是感知不到的，它处于等待状态，发送方如果不设置计时器，也会一直等待对方的ACK，此时，死循环发生了。超时机制的引入，打破了死循环，让传输可以继续下去。

RTO的计算：RTO应该略大于RTT。我们都知道RTT是Round Trip Time，即往返时间，如果按照一个数据包一个ACK的模式，发送方最好需要等待略大于RTT的时间内，没收到ACK，才认为需要重传。如果RTO小于RTT，则发生无效的重传，如果RTO远大于RTT，则由于等待时间过长，带宽得不到很好的利用。

针对一条连接中网络的状况是不断发生变化的，RTT也会由于路由器的队列长度而产生波动，所以RTO也是动态的，以适应这种变化。

RFC793

在第一版的TCP RFC793中，需要采样最新的一次RTT，同时维护一个平滑RTT(SRTT)的值，每次采样到了最新的RTT，就会更新SRTT，SRTT用来计算RTO：

SRTT = (α * SRTT) + ((1- α) * RTT)，0.8<α<0.9

RTO = min[UBOUND, max[LBOUND, (β * SRTT)]]，1.3<β<2.0

Karn算法

上述算法存在一个问题，在采样RTT的时候，涉及重传的RTT是否需要采样？

因为我们不知道第一个收到的ACK究竟是对原始数据包的确认，还是对重传数据包的确认，不管采用前者还是后者，计算出的RTT都是不准确的。Karn算法直接跳过对涉及重传的RTT的采样（此处的涉及两字，是为了表述不对原始数据包、重传数据包和第一个ACK做采样）。

但Karn算法有一个严重的问题，假设这样一个场景，发送方同时发送了几个数据包，RTO刚开始是较小的（假设200ms），但网络负担突然加重，延时增加，RTT变为1000ms，由此发送方在200ms超时后重传所有数据包，而由于Karn算法不对涉及重传的RTT采样，所以SRTT是不更新的，由此RTO也不会更新，发送方无法更新RTO来适应网络的变化，而是继续无谓的重传，同时加重网络的负担。

为了解决这个问题，Karn算法提出每次超时重传后，重置RTO为之前的两倍，这也是我们今天仍在使用的机制。

Jacobson算法

上述两个算法使用SRTT，但由于0.8<α<0.9，可以发现SRTT对历史值的依赖度很高，对最新采样的RTT的权重很低，这就导致了它无法及时检测RTT大的抖动，如果网络环境就此发生较长期的变化，那么SRTT需要在多次RTT之后，才能更新到接近真实的RTT，这增加了自适应的时间，如果RTT减少较多，则无法及时降低RTO，而浪费了带宽，如果RTT增加较多，则无法及时增加RTO，从而增加了重传。

SRTT = SRTT + α * (RTT – SRTT)

DevRTT = (1-β) * DevRTT + β * (|RTT-SRTT|)

RTO= µ * SRTT + ∂ * DevRTT

Linux使用的上述公式的参数是α = 0.125，β = 0.25，μ = 1，∂ = 4

带入到RTO计算公式，可知RTO对DevRTT的考虑是充分的，而DevRTT对|RTT-SRTT|的考虑虽然只有0.25，但加上RTO公式中∂=4的放大，对RTT差值的考虑是较为充分的，即可以及时检测RTT大的抖动，并调整RTO适应网络环境。

1.5 滑动窗口

同时，如果TCP采用最原始的一次数据传输一次ACK后，才能继续发送，则吞吐量是很低的，很多时间都在等待ACK中度过。为了提高网络的吞吐量，TCP引入窗口的概念，窗口是不等待ACK，而可以发送的最大数据量。发送方窗口如下：
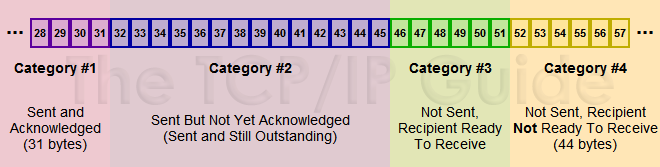
tcp-send-window
(来源：《The TCP-IP Guide》)

#1 已发送已确认这部分数据不再维护发送窗口外缓冲区外

#2 已发送未确认缓冲区内（需要保存这些数据，以备重传）发送窗口内

#3 未发送在接收方可处理范围内规定了上层应用可以发送的数据量缓冲区内发送窗口内

#4 未发送上层应用可以继续填满缓冲区这部分数据不在接收方可处理范围内缓冲区内发送窗口外

在接收到ACK（累计确认）后，发送方窗口左边界右移，经过确认的数据不再维护。窗口的右边界是否移动，则取决于接收方ACK中报告的窗口大小，如果窗口不变，表明接收方处理了这些字节，发送方右边界右移这么多字节，如果窗口变小，则说明接收方处理较慢，发送方根据这个窗口调整发送窗口即可。
窗口左右移动的过程，称为「滑动」。

在接收方，窗口的示意图如下：
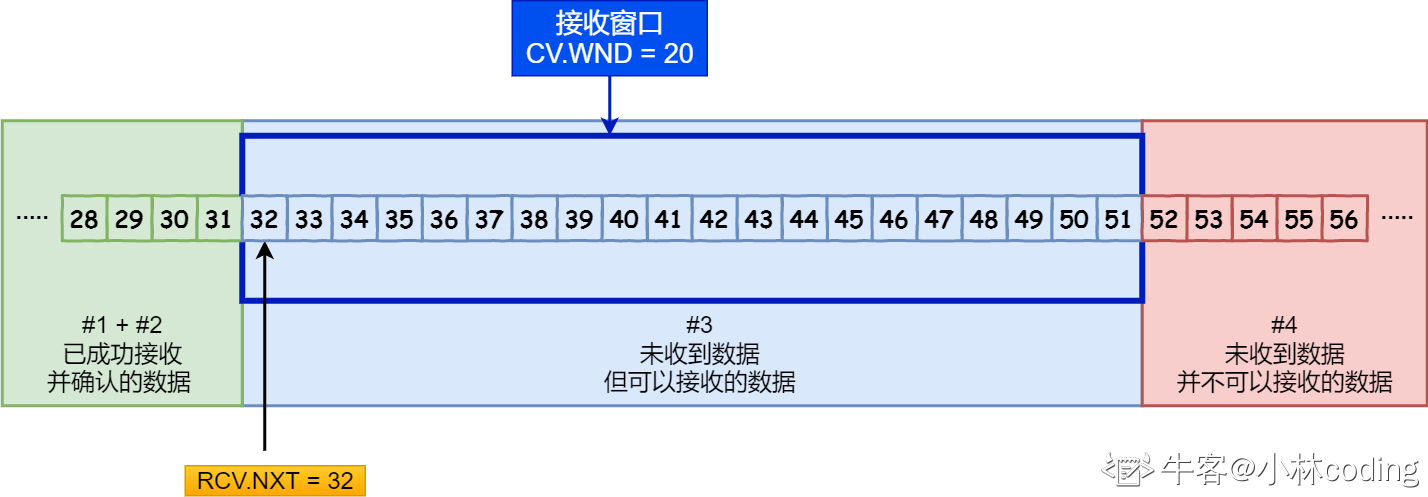
tcp-recv-window
(来源：小林coding)

#1#2 已接收如果有ack丢失的对方重传后回一个dup ack即可缓冲区内

#3 未接收但可以接收这部分等于接收窗口的大小缓冲区内

#4 未接收缓冲区外这意味着只要上层应用读取了#1#2中的数据，接收窗口的右界就会右移，即有更多的缓冲区可以接收数据，相应的，接收窗口的大小也会扩大

接收方的窗口要简单一些，窗口大小就是#3，需要注意的是，#1#2中的数据会保存在缓冲区，等待上层应用读取后再回收，如果上层应用一直不读取，随着数据的接收，缓冲区大小会减少为0，此时可接收窗口大小也是0，接收方会马上回复一个window=0的ACK报文。此时发送方停止发送数据，并每个一段时间发送一个Zero Window Probe探测报文(Len=1，但对方不需要对这个序列号确认)，接收方回复Zero Window Probe ACK报文，及时报告窗口大小，如果有可用窗口，发送方就继续发送数据。

此处就引入了糊涂窗口综合征(Silly Window Syndrome)的概念，如果接收方在接收窗口为0后，上层应用处理了很少的几个字节，就报告窗口给发送方，发送方立即发送这几个字节，则数据的传输效率是很低的，这里Header(Ethernet 14 + IP 20 + TCP 20)就有54字节，只传送几个字节的有效数据，是低效的。

类似的问题也会发生在接收方，如果接收方的窗口越来越小，每次发送的数据越来越少，数据的传输效率就越来越低，以至于不值得这么做。

上述两种症状称之为糊涂窗口综合征。如何解决？分别在接收方和发送方解决即可：

1.接收方不报告小窗口，而是等到可接受窗口大小>=MSS时，才报告窗口变化。

2.发送方不发送小数据，著名的Nagle算法就是这么做的，即在窗口大小>=MSS并且可发送数据>=MSS时，才发送数据，如果不满足这个条件，则检查所有已发送数据的ACK是否收到，只有收到才发送数据，否则缓存上层应用的数据。

需要注意，Nagle算法由于延迟发送的特性，它跟延迟确认(Delayed ACK)算法是水火不容的。在发送方上层应用发送小数据时，TCP会缓存这些小数据，直到之前所有数据的ACK都接收到，但延迟确认则正好相反，既然多次ACK是一种浪费，那我就等待下一次数据到达后再发送ACK。这样，发送方等待对方的ACK，接收方等待对方的下一次数据，这就死锁了。

另外，Nagle算法由于会缓存小数据，而一些特定的交互场景，如应用层的SSH等，本身就需要快速传输小数据，那么就需要关闭Nagle，具体是在setsockopt中设置TCP_NODELAY的选项。

2.流量控制

发送方不能发送超过接收方处理能力的数据，这就是流量控制要做的。
TCP基于滑动窗口，实现对数据的高效发送，基于发送方报告窗口的机制，得知当前可发送窗口的大小，来控制发送方的发送速度。
其他内容在滑动窗口一节已经介绍。

3.拥塞控制

拥塞控制是独立于流量控制的，流量控制的目的，是让发送方不会发送超过接收方处理能力的数据，这是收发双方的事情，而拥塞控制则考虑到了链路的状况，即是否发生了拥塞。一旦检测到发生了拥塞，TCP就会通过拥塞控制算法，降低发送速率，网络中的用户都会在拥塞发生后，主动降低自己的发送速率，而不是保持发送速率，否则将会给路由器造成更大的压力，造成RTT增大，丢包剧增，丢包导致的重传，会继续加重网络的负担，最终让整个网络崩溃。

而降低发送速率，则给链路中的瓶颈路由器增加处理的时间，等路由器处理掉排队数据包之后，网络就会恢复正常，此时TCP再增加发送量即可。

那如何做具体的拥塞控制呢？主要有四个算法：慢启动，拥塞避免，拥塞发生，快速恢复，英文版Congestion Control的介绍在RFC2001。

首先介绍拥塞窗口(Congestion Window，简称cwnd)，发送方窗口swnd = min(rwnd, cwnd)，这里cwnd也能限制发送方发送数据的行为。cwnd默认以MSS为单位，MSS在以太网中一般设置为1460。

慢启动

TCP三次握手，开始发送数据时，首先从cwnd=1开始发送，然后每接收到一个ACK，cwnd加1，在一个RTT后，cwnd等于2，此时可以连续发送两个MSS，又过了一个RTT，发送方接收到了两个ACK，则变更cwnd=2+2，此时可以连续发送四个MSS，又过了一个RTT，接收到四个ACK，则cwnd=4+4…

慢启动过程就是每个RTT后，cwnd都翻倍，直到到达慢启动阈值(ssthresh, slow-start threshold)，随之进入拥塞避免阶段。

为什么要进行慢启动？因为刚加入网络的TCP代理并不知道网络的状况，所以就从一个很低的cwnd逐渐增长，来探测网络的状况。

相对于直接发送大量的数据包，慢启动是一个温和的过程，不会对网络中其它TCP代理造成很大的抖动，其它代理检测到网络拥塞后，也可以温和地调整拥塞窗口大小（而非一个新加入的TCP代理大量发包，导致路由器队列满，其它代理丢包超时重传，这个影响是很大的，如果用传统的拥塞发生算法（如下），则直接cwnd重置为1）

拥塞避免

拥塞避免算法是为了当cwnd大于等于ssthresh时，进入拥塞避免阶段，发送方每接收一个ACK，cwnd+=1/cwnd，这就意味着，在一个RTT后，cwnd=cwnd+1，即随着RTT的增加，cwnd线性增加。

这种线性增加的算法称之为加性增(Additive increase)，与之对应的拥塞发生算法是乘性减(Multiplicative decrease)，它们合称为AIMD。使用这种控制算法的好处是共享链路中的所有TCP流，都可以最后收敛到均分带宽的目的。(from Wikipedia: Multiple flows using AIMD congestion control will eventually converge to use equal amounts of a contended link.)

回到拥塞避免上，当cwnd随着RTT缓慢增长时，总会遇到一个极限，因为链路中总会存在一个瓶颈路由器，它的处理能力是有限的。但这个路由器的队列满，就开始丢包，发送方在RTO内没有接收到ACK，就会重传，此时进入拥塞发生时对超时重传的处理阶段。

另外，如果发送方收到了3个重复的ACK(duplicate ACK)，则进入拥塞发生时的快速重传和快速恢复阶段。

拥塞发生

早期TCP对拥塞发生的判断是基于丢包的。

一旦丢包，就会进入拥塞发生算法，有两种机制处理拥塞的发生，一种是针对超时重传，此时TCP认为网络发生了较为严重的拥塞，就会马上降低发送速度，具体是设置ssthresh=cwnd/2，cwnd=1，也就是说，从头开始慢启动，到之前慢启动门限的一半，再进入拥塞避免阶段。

快速恢复和快速重传

另一种是针对快速重传，此时TCP认为既然丢失的包之后的三个不同的包都收到了，说明网络的拥塞没那么严重，此时TCP会降低发送速度，但降低得没超时重传那么大，具体是设置ssthresh=cwnd/2, cwnd=ssthresh+3，为什么是加了3，因为三个重复ACK已经收到了。

接下来算法的过程如下：
1.每当收到了重复ACK，cwnd加1；
2.新的ACK到达，说明前面快速重传的数据包被接收，此时设置cwnd=ssthresh，进入拥塞避免阶段。这里我看不明白，既然已经接收到新的ACK，为什么cwnd反而降低了？

拥塞控制中的信号

拥塞控制中的信号(signal)概念，在1988年SIGCOMM的论文《Congestion Avoidance and Control》中，作者写道：拥塞控制的条件有两个，其一是网络必须有能力通知(signal)终端(endpoints)，拥塞已经发生或将要发生，其二是终端必须实现拥塞控制的策略，以在信号到达时降低发送速率，在信号消失时，提高发送速率。

我们结合上述介绍的传统算法，把丢包看成是一个发生拥塞的信号，丢包发生时，降低发送速率，丢包消失时（每次接收到ACK可以看成是与丢包相反的信号），提高发送速率。

这里的丢包是一种大概率的丢包，比如说，在网络中，丢包有三种情况：1.路由器丢包，发生拥塞，2.时延突然增大导致RTO超时，3.数据包在噪音信道中极小概率的被破坏。

第三种情况可以忽略，因为概率太小了，远小于1%，这还只是当时的网络环境的测量结果。第二种情况也可以忽略了，超时应该尽快重传，而不是等待这个数据包在环游网络的某个神奇的时刻到达，所以如果丢包，我们可以认定就是路由器丢包，网络发生了拥塞。

而RTO是根据RTT动态维护的，如果我们有一个合理的RTO，就可以等同于认为只要RTO超时，就发生了丢包。另一种关于丢包的假设是在发送方收到三个重复ACK时，重复ACK是用来指示乱序到达的，如果只收到了一个或两个重复ACK，很有可能只是乱序，并没有丢包，此时TCP是不会触发快速重传的，它在等待更多的重复ACK到达。如果更多(大于等于三个)的重复ACK收到，则丢包的概率就很大了，此时触发快速重传就比较合理了。

关于拥塞控制算法，根据Jacobson关于拥塞控制的两个条件，我们还可以想到更多的拥塞控制算法，比如，基于时延(Delay)的拥塞控制算法，如大名鼎鼎的BBR，基于路由器主动通知的拥塞控制算法，如ECN(Explicit Congestion Notification, 显示拥塞通知)。此外，基于丢包(Loss)的拥塞控制算法有很多改进版本，如被Linux使用的BIC、CUBIC等。

参考文献：

1.Jacobson，1988，Congestion Avoidance and Control

2.陈皓，TCP那些事儿

3.小林coding，TCP重传、滑动窗口、流量控制、拥塞控制

4.ricardoleo，TCP协议-如何保证传输可靠性

5.陶辉笔记，关于路由器队列

6.Wikipedia: AIMD

7.henrystark，AIMD：公平性和收敛性

8.Wikipedia: 常见的拥塞控制算法一览表

2020-04-27

不重复元素的全排列

问题描述

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

来源：LeetCode

解法一

回溯的基本框架：1.当前已走路径，2.当前可选路径列表，3.结束条件（符合条件或到达决策树底部）。在回溯函数内，for循环可选路径。

时间复杂度：有N!个不同的排列（N!次调用回溯函数），每个排列复制到结果集合，需要O(N)，所以最后时间复杂度为O(N*N!)

严格按照框架写，如下：


``

## 解法二
同样利用回溯法，在全排列中，当前路径保存在nums[0,begin-1]中，可选路径列表为[begin,end]，则for循环[begin,end]，最后begin=end，本次回溯结束。

```c++
class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> res;
        int n = nums.size();
        helper(res, nums, 0, n-1);
        return res;
    }

    void helper(vector<vector<int>> & res, vector<int> & nums, int begin, int end) {
        if(begin == end) {
            res.push_back(nums);
            return;
        }
        for(int i = begin; i <= end; i++) {
            // 做选择
            swap(nums[i], nums[begin]);
            helper(res, nums, begin+1, end);
            // 撤销选择到原始状态
            swap(nums[i], nums[begin]);
        }
    }
};

2020-04-27

子集

问题描述

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]

来源：LeetCode

解法一

对于子集问题，对每一个元素，我们都有选和不选两种选择，如何模拟这两种选择？可以使用递归回溯，递归参数保存了当前待访问的元素索引，临时子集保存在vector中，递归出口是当前待访问的索引为数组的长度，则保存临时子集的结果。

回溯法是一种递归寻找符合要求的解的方法，适用的问题是决策树类型，即在决策树怎么一步一步遍历。回溯的框架需要考虑三个变量：1.当前已走路径，2.当前可选路径列表，3.结束条件（符合条件或到达决策树底部）。

在下述代码中，have保存当前已走路径，可选路径只有两条，那就是对当前元素，走还是不走。不走，则对应一个回溯函数，回溯到底部，并保存结果；走，则保存当前元素到have中，回溯返回后，对撤销have中已选的当前节点，回到上一个状态（为什么撤销，这里have是引用类型，是为了节省形参内存，不是引用类型，那么撤不撤销都不会影响下一次选择）

时间复杂度：有2^{n个子集（2}n次调用回溯函数），每个子集复制到结果集合，需要O(n)，所以最后时间复杂度为O(n*2^n)

class Solution {
public:
    vector<vector<int>> res;
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<int> have;
        helper(nums, have, 0);
        return res;
    }

    void helper(vector<int>& nums, vector<int> & have, int index) { // from 0
        if(index == nums.size()) {
            // 递归出口 保存结果
            res.push_back(have);
            return;
        }
        helper(nums, have, index+1); // 不使用当前元素
        have.push_back(nums[index]); // 使用当前元素
        helper(nums, have, index+1);
        // 当前选择不会对下一次选择产生影响
        have.pop_back(); // 每次have在helper输入输出中是不变的
    }
};

Spark Era Coming...

分享技术记录生活

复杂链表的复制

问题描述

解法一

滑动窗口的最大值

问题描述

解法一

详解DES加解密

密码保存里的学问

linux-init

理解HTTPS协议

Nginx事件驱动框架

关于TCP的一切

1.差错控制

1.1 校验和

1.2 序列号

1.3 确认应答机制

1.4 超时重传

RFC793

Karn算法

Jacobson算法

1.5 滑动窗口

2.流量控制

3.拥塞控制

慢启动

拥塞避免

拥塞发生

快速恢复和快速重传

拥塞控制中的信号

不重复元素的全排列

问题描述

解法一

子集

问题描述

解法一