DES(Data Encryption Standards)是一种经典的对称加密技术，由IBM公司在1970s研发，之后被美国国家标准局标准化。在理解DES之前，我们先补充对称加密的基本思想。

对称加密是加解密使用同一个密钥的加密算法，区别于使用公钥和私钥加解密的非对称加密。同时，按照对称加密的密钥特征，分为流密码(stream cipher)和分组密码(block cipher)，前者每次加密数据的一个位或一个字节，后者则每次加密一个固定大小的块，即先把数据分块，再分别用密钥加密。流密码的代表是RC4，分组密钥的代表则是DES和AES。

现代密钥学只对密钥保密，算法是公开的。因为基于算法的保密随着算法的推测或暴露而消失，同时算法不公开，也难以对算法进行讨论和改进。

一个好的密码系统要能够对抗基于统计方法的密码分析(Statistical cryptanalysis)，比如在选择明文攻击和选择密文攻击得到的明文和密文对中，统计明文和密文的规律，根据密文破解明文，另外，还可以通过分析密文和密钥的对应关系，从而破解密钥。

对抗统计分析攻击的方法是，设法使明文的统计特征尽可能的不带入密文，同时使密文和密钥的统计关系尽量复杂，这样攻击者就很难统计出有效的规律，来推断明文和密钥。

在历史上，这种思想早就有了。信息论的先驱香农在1945年的论文《密码学的数学理论》中给出了设计密码系统的基本方法：混淆(confusion)和扩散(diffusion)。混淆是把密钥和密文的统计关系打乱，使得密钥极其微小的改动，都会造成密文的大幅变动；扩散则把明文和密文的统计关系打乱，使得明文极其微小的改动，都会造成密文的大幅变动，换言之，明文的任意部分都会影响密文的所有部分，这让密码分析者难以找到明文到密文的部分模式，因为模式被上述方式抹掉了。

这种明文和密钥的微小改动，所造成的密文大幅变动，就是雪崩效应(avalanche effect)：

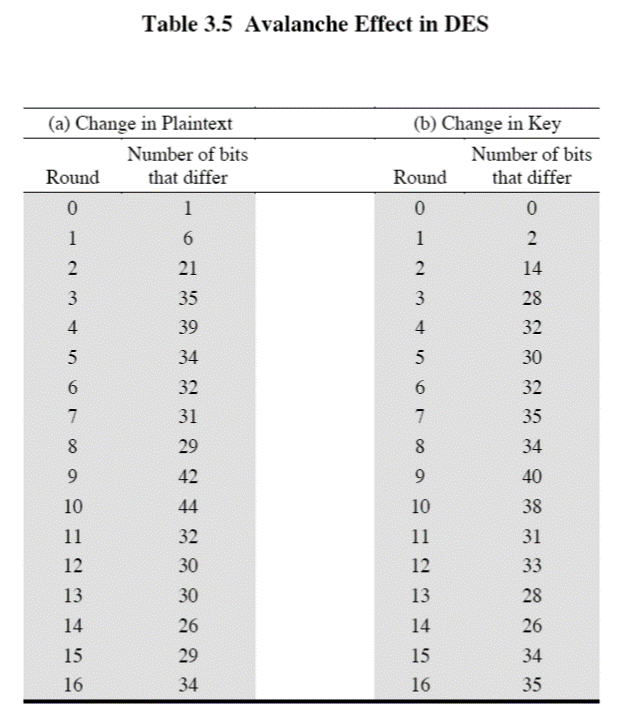
对应到DES的设计，主要是具有雪崩效应的Feistel网络，这是DES的核心，也是后续很多对称加密的核心(如Blowfish、RC5)。

Feistel网络如下：

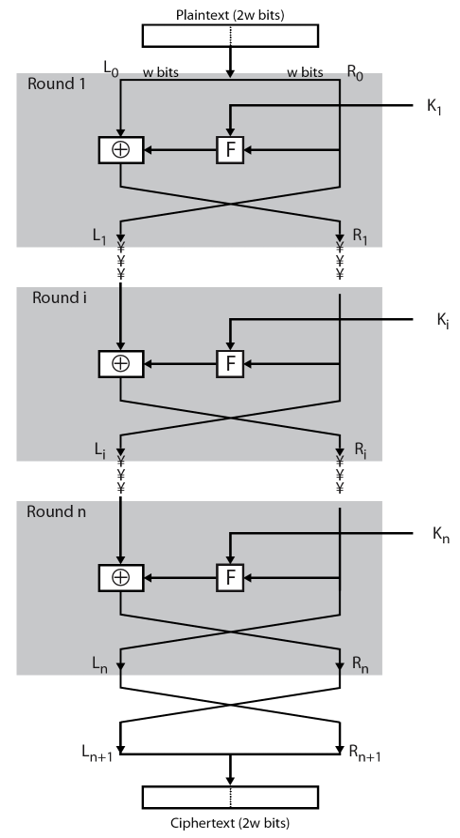
首先说明，DES的分块长度是64位，密钥长度是64位，其中有效密钥的长度是56位，另外的8位用作奇偶校验。DES分块的密文长度是64位。上图的L0和R0分别是64位明文经过初始置换后的左32位和右32位，之后进入16轮的迭代，最后再经过与初始置换的逆置换，来得到最终的密文。

每一轮的具体流程如下：

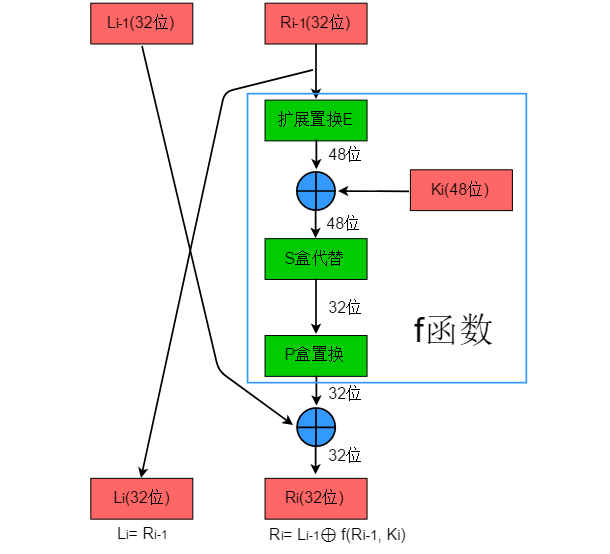
(来源)

在每轮迭代中，DES都使用相同的加密结构，这种结构就是Feistel结构。公式如下：
$L_i = R_{i-1}$
$R_i = L_{i-1} ⊕ f(R_{i-1}, k_{i-1})$

其中f是feistel函数。每轮除了一些置换(Permutation)外，最核心的是S盒的替代(Substitution)。置换是改变位的顺序，一般使用预置的置换表，替代则通过一定的规则，把数据替代成新的数据。

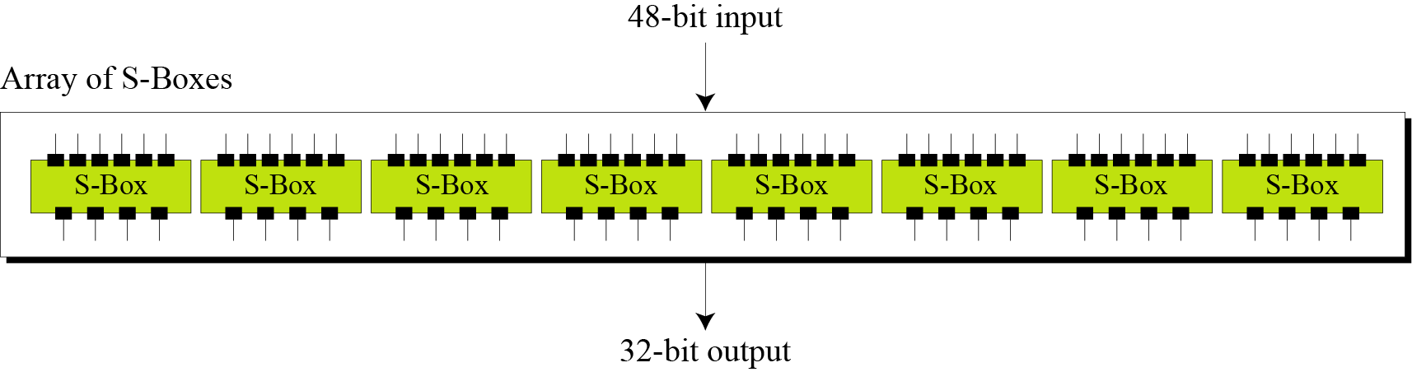
S盒是DES中唯一的非线性部件，S盒的设计从根本上决定了每一轮能否制造足够的复杂性。有了非线性部件，通过多轮迭代，我们就可以得到不断扩散，使得每一轮具有一定随机性的加密输出的每一位，都继续参与下一轮的扩散，结果就是，明文的微小改动，都会经过多轮扩散的放大，最终体现在密文中。(stackoverflow上的解释是：Changing a single bit in the input will cause more bits to be changed in the following rounds.)

关于S盒，如果我们再仔细一点，会发现它的功能是完成6位数据到4位数据的压缩，如果我们得到了4位的S盒输出，想反推出6位的输入，就有四种可能。可以类比一下，当我们知道了密文，想反推出明文，每一轮都有四种可能，4^16次方，那是有多少种可能的明文啊！况且还有密钥的加持。

S盒的作用不仅仅在扩散，因为S盒的输入是每轮密文的Ri和轮密钥Ki，就算不用轮密钥，只使用原始密钥，每次经过非线性的S盒，也会增加混淆的程度。何况为了更好的安全性，DES专门生成了每轮的密钥。

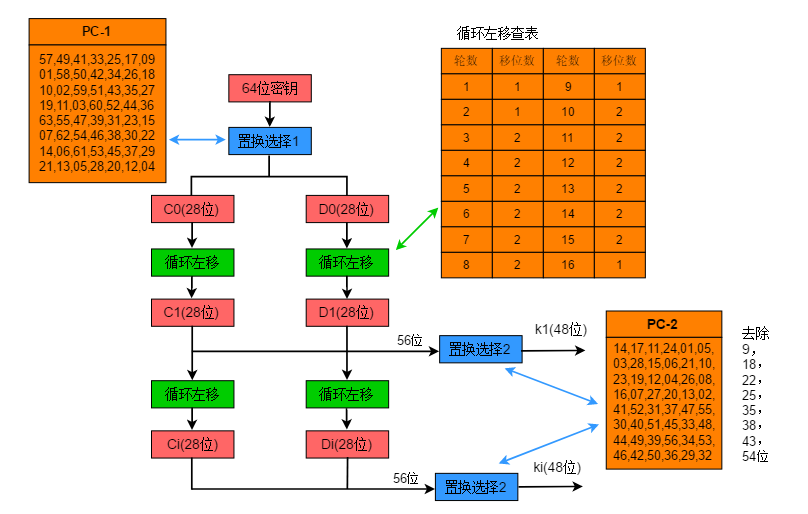
(来源)

按照我的理解，轮密钥增加了密钥和密文关系的复杂性，即增加了DES的混淆能力，因为每一位原始密钥的变化，都会通过轮密钥迭代的形式，放大到所生成的所有密钥里。此后，轮密钥与上一轮的加密输出异或后，进入S盒，所以最后的结果是混合了密钥和明文每个位的影响的，就如同蝴蝶效应一样。

分析了DES的Feistel网络的优点，我们来看整个加密流程：

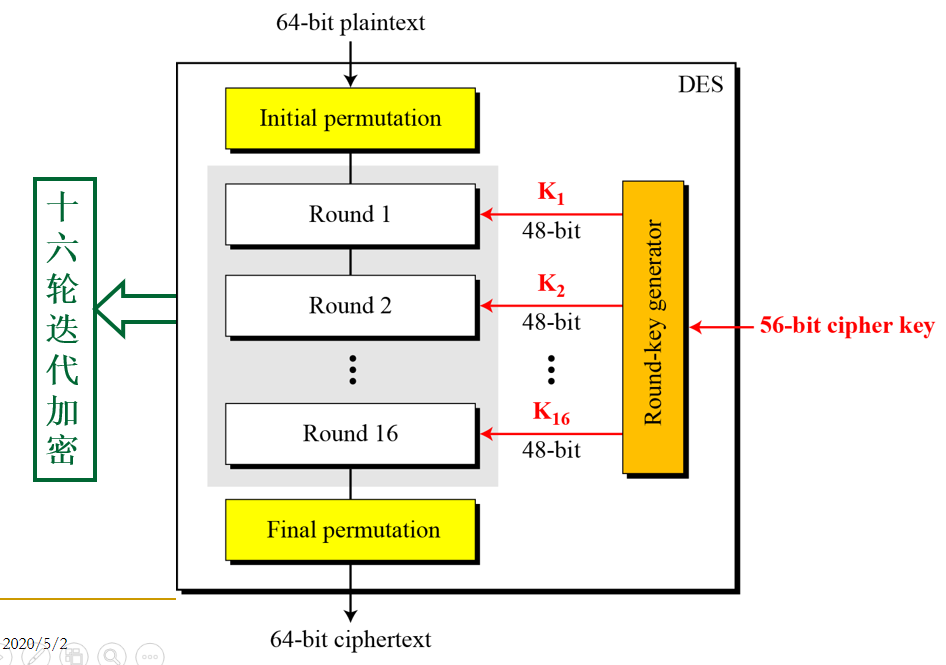
DES首先了对分组明文做了初始置换(Initial Permutation)，最后结束的时候，对密文做了逆初始置换(Inverse Initial Permutation)。

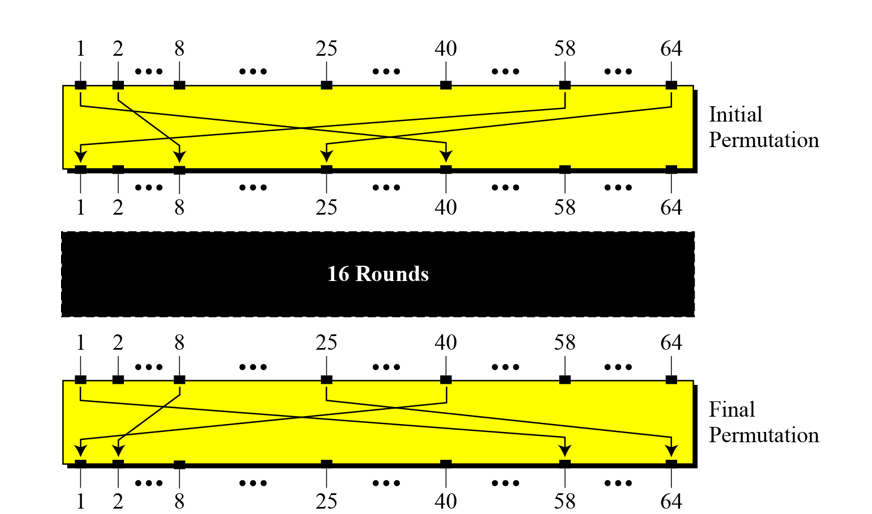
这部分对混淆和扩散没有作用，那为什么还要这两个置换呢？其实这是历史原因，当时DES标准的提交者为了降低硬件实现DES的复杂性，而多了这个设计，所以标准化之后，这个初始置换就留下来了。参见What are the benefits of the two permutation tables in DES?

仔细看的话，会发现后者是把每一位放回到最开始的位置，按照我的理解，这是为了让解密过程也能复用加密的框架。因为解密除了反向使用轮密钥外，其它的过程与加密是一致的。

DES解密是加密的逆过程，上面介绍了初始置换和逆初始置换是逆过程，剩下就是证明16轮迭代解密是16轮迭代加密的逆过程。

这里用到了异或(xor)的重要性质，a⊕a=0, a⊕0=a，考虑一个基本的密码形式，p是明文，c是密钥，e是密文，通过明文和密钥按位异或得到，p⊕c=e，接收方得到密文后，异或密钥解密：e⊕c=p⊕c⊕c=p

每轮解密，我们需要用$L_i$和$R_i$，解密出上一轮的$L_{i-1}$和$R_{i-1}$

回顾一下加密公式：
$L_i = R_{i-1} \qquad \qquad \qquad \qquad (1)$
$R_i = L_{i-1} ⊕ f(R_{i-1}, k_{i-1}) \ \ \ (2)$

解密公式为：
$L_{i-1} = R_i ⊕ f(L_i, k_{i-1}) \ \ (3)$
$R_{i-1} = L_i \qquad \qquad \qquad \ \ (4)$

把(2)带入到(3)中，则有：
$L_{i-1} = L_{i-1} ⊕ f(R_{i-1}, k_{i-1}) ⊕ f(L_i, k_{i-1})$

再把(4)带入上式：
$L_{i-1} = L_{i-1} ⊕ f(L_i, k_{i-1}) ⊕ f(L_i, k_{i-1}) = L_{i-1}$

这里最后推导出相等，说明按照相同的结构，用下一轮的密文，就可以回推到上一轮密文，最终迭代回明文。只不过这里交换了L和R的顺序，迭代函数的框架可以复用。

写到这里，DES这么经典的算法，的确很经典，Feistel结构，S盒的设计，简单的多轮迭代增加混淆和扩散的思想，都让我感受到DES算法的简洁和经典之美。

PS: 文中如有错误，欢迎指出，本站不胜感激。版权给hackeryard所有，转载请注明出处。

参考：

1.程序员小吴，神秘的DES加密算法

2.nnnnzyx，DES解密是加密的逆过程

3.Wikipedia: Feistel cipher

4.Wikipedia: Confusion and diffusion

5.西电计算机密码学课PPT